🔗 15684번 : 사다리 조작
● Java 풀이
● 시간 제한 2초
● 메모리 제한 512 MB
문제
사다리 게임은 N개의 세로선과 M개의 가로선으로 이루어져 있다. 인접한 세로선 사이에는 가로선을 놓을 수 있는데, 각각의 세로선마다 가로선을 놓을 수 있는 위치의 개수는 H이고, 모든 세로선이 같은 위치를 갖는다. 아래 그림은 N = 5, H = 6 인 경우의 그림이고, 가로선은 없다.
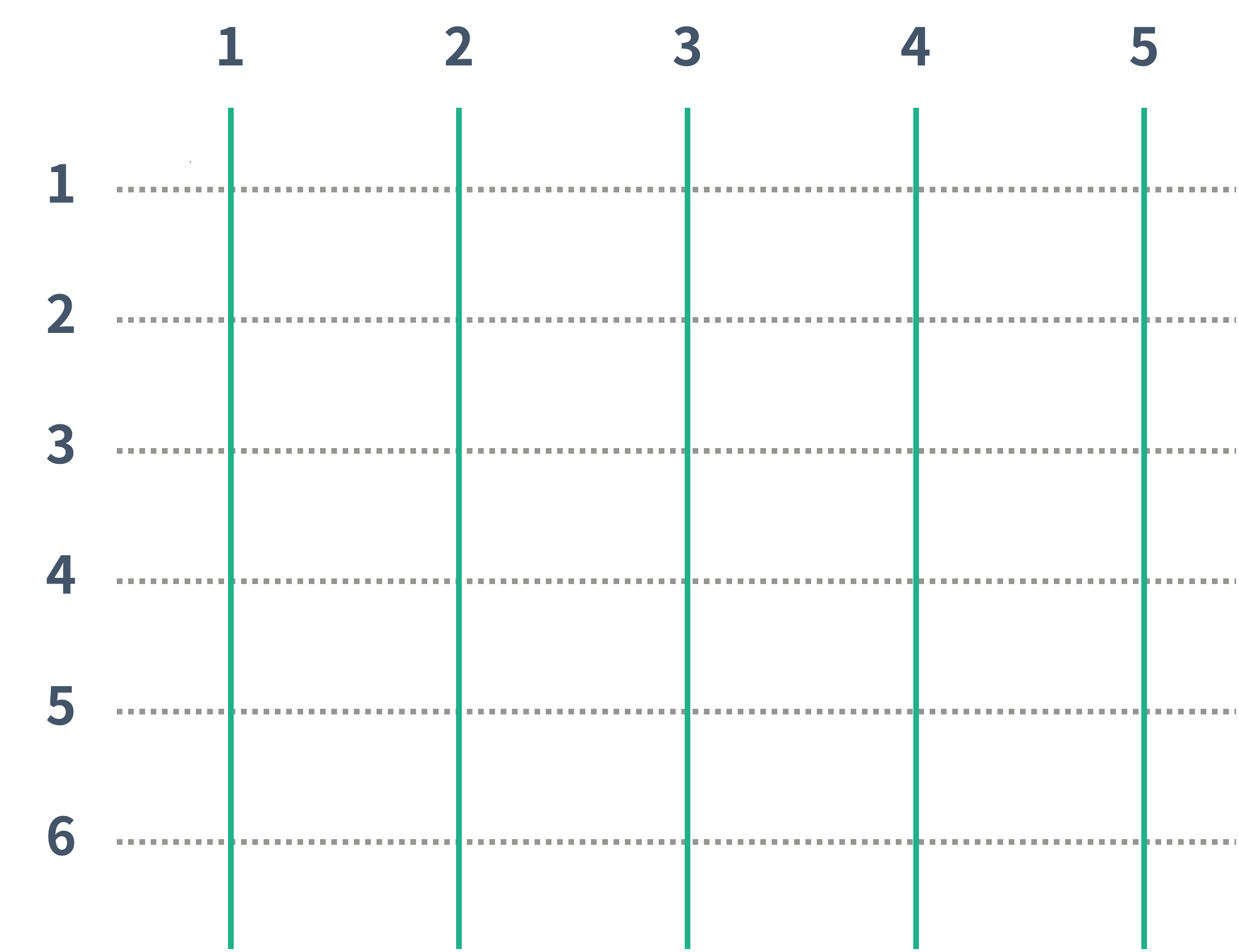
초록선은 세로선을 나타내고, 초록선과 점선이 교차하는 점은 가로선을 놓을 수 있는 점이다. 가로선은 인접한 두 세로선을 연결해야 한다. 단, 두 가로선이 연속하거나 서로 접하면 안 된다. 또, 가로선은 점선 위에 있어야 한다.
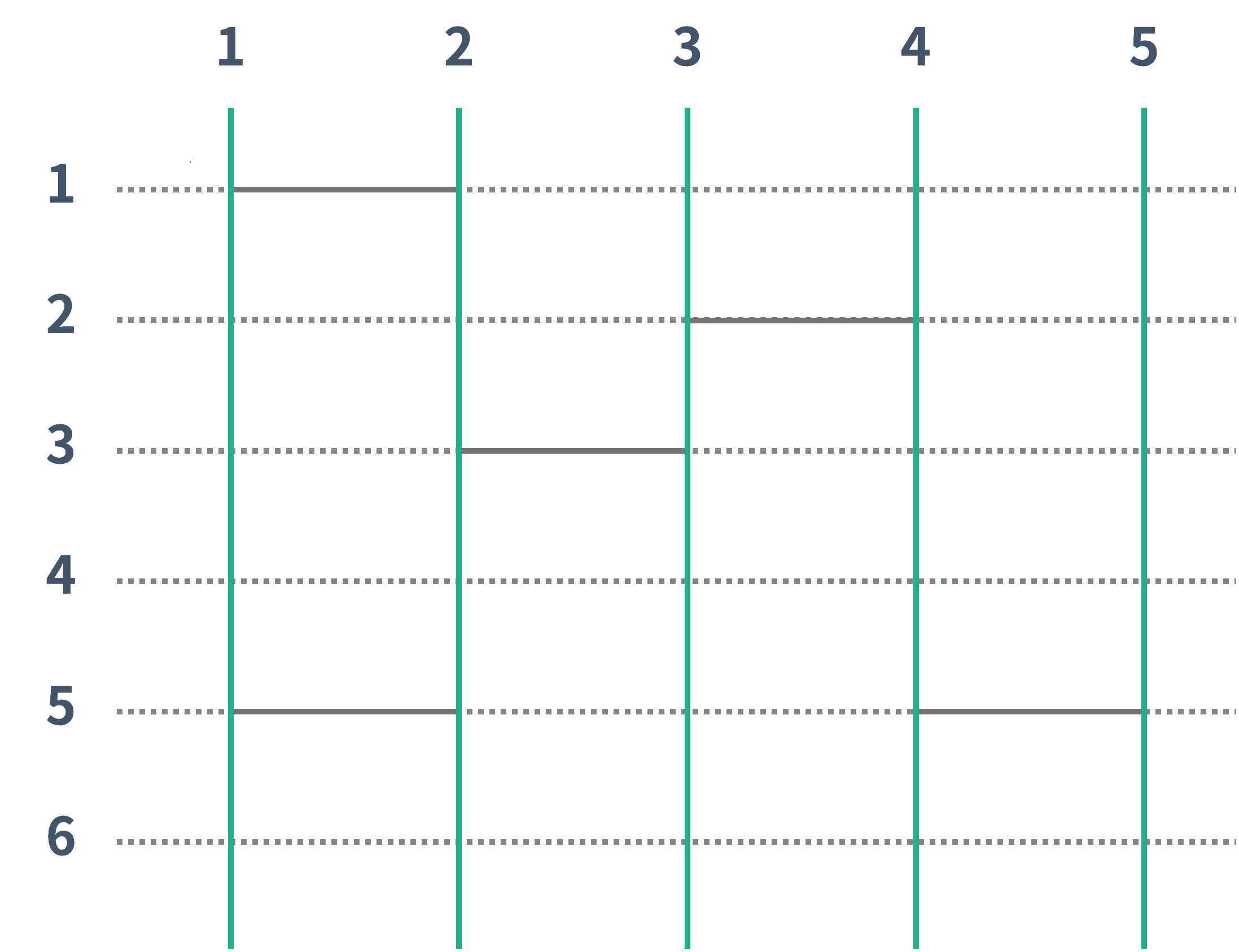
위의 그림에는 가로선이 총 5개 있다. 가로선은 위의 그림과 같이 인접한 두 세로선을 연결해야 하고, 가로선을 놓을 수 있는 위치를 연결해야 한다.
사다리 게임은 각각의 세로선마다 게임을 진행하고, 세로선의 가장 위에서부터 아래 방향으로 내려가야 한다. 이때, 가로선을 만나면 가로선을 이용해 옆 세로선으로 이동한 다음, 이동한 세로선에서 아래 방향으로 이동해야 한다.
위의 그림에서 1번은 3번으로, 2번은 2번으로, 3번은 5번으로, 4번은 1번으로, 5번은 4번으로 도착하게 된다. 아래 두 그림은 1번과 2번이 어떻게 이동했는지 나타내는 그림이다.
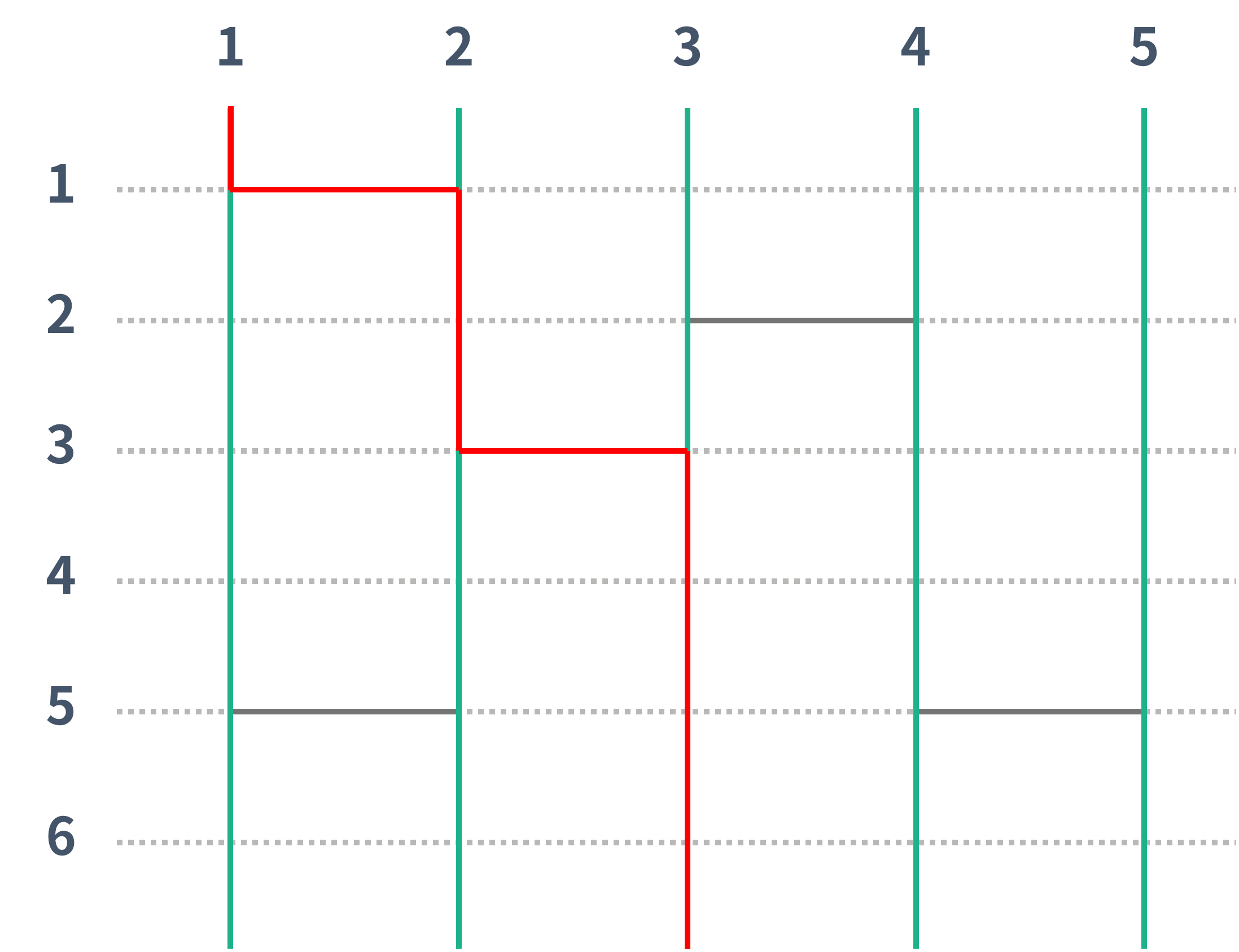
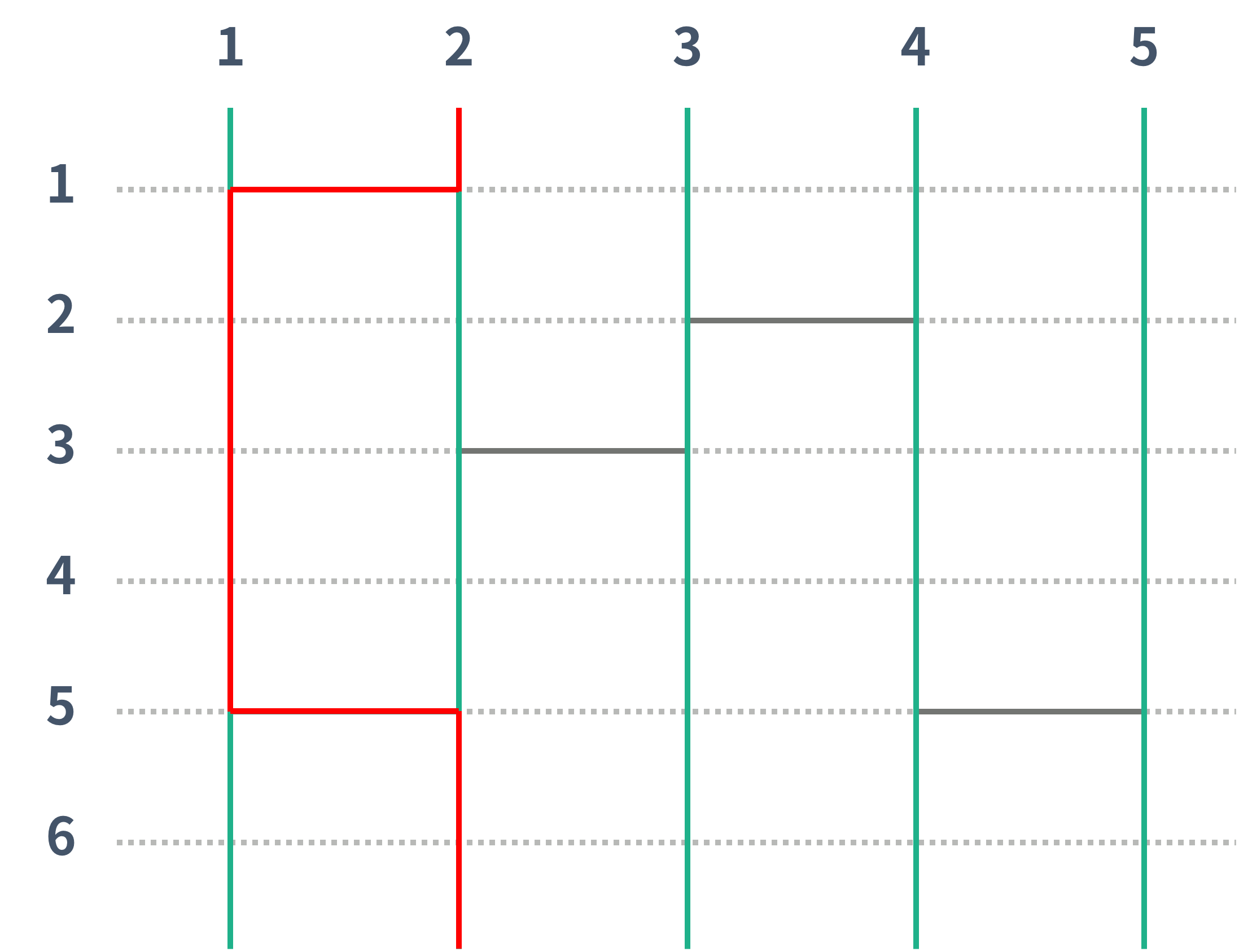
| 1번 세로선 | 2번 세로선 |
사다리에 가로선을 추가해서, 사다리 게임의 결과를 조작하려고 한다. 이때, i번 세로선의 결과가 i번이 나와야 한다. 그렇게 하기 위해서 추가해야 하는 가로선 개수의 최솟값을 구하는 프로그램을 작성하시오.
테스트 케이스
// input
3 3 3
1 1
2 2
3 1
// answer
-1
// input
3 2 3
1 1
3 1
// answer
0
// input
3 3 3
1 2
2 2
3 2
// answer
-1
/** 출처 (https://www.acmicpc.net/board/view/135611) **/
// input
4 3 4
1 1
2 2
1 3
// answer
3
// input
4 1 4
3 2
// answer
1
// input
2 0 3
// answer
0
// input
2 1 3
1 1
// answer
1
// input
5 5 6
1 1
3 2
2 3
5 1
5 4
// answer
3
// input
2 0 1
// answer
0
// input
2 0 2
// answer
0
// input
2 1 2
1 1
// answer
1
// input
2 2 2
1 1
2 1
// answer
0
// input
2 3 4
1 1
2 1
3 1
// answer
1
풀이
import java.io.*;
import java.util.*;
public class Main {
private static int N, M, H, MIN_BRIDGE; // 사다리 세로선, 가로선, 가로선 가능 개수
private static boolean[][] verticalLines; // 가로선 존재 여부
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
H = Integer.parseInt(st.nextToken());
MIN_BRIDGE = 4; // INF 값 정의
verticalLines = new boolean[H + 1][N + 1]; // 가로선 위치 표기할 배열
for (int i = 0; i < M; i++) { // 주어진 가로선 위치 표기
st = new StringTokenizer(br.readLine());
verticalLines[Integer.parseInt(st.nextToken())][Integer.parseInt(st.nextToken())] = true;
}
boolean flag = true; // 사다리를 탔을 때 i번 출발점이 i번 도착점을 가리키는지
for (int i = 1; i <= N; i++) { // 가로선을 하나도 놓지 않았을 때
if (!canStraight(i, i, 1)) { // 가리키지 않는 경우
flag = false; // false 설정
break;
}
}
if (flag) { // (1-n) 출발점이 모두 (1-n)번 도착점을 가리킬 경우 (false에 걸리지 않았을 경우)
System.out.println(0); // 가로선을 하나도 안 놓아도 됨
return;
}
selectBridge(1, 1); // 1개부터 3개까지의 가로선 선택 (완전 탐색)
System.out.println(MIN_BRIDGE == 4 ? -1 : MIN_BRIDGE);
}
private static void selectBridge(int count, int r) {
boolean flag; // 사다리를 탔을 때 i번 출발점이 i번 도착점을 가리키는지를 나타낼 flag 변수 선언
for (int i = r; i <= H; i++) { // 가로선 탐색
for (int j = 1; j < N; j++) { // 세로선 탐색
if (!verticalLines[i][j] && !verticalLines[i][j - 1] && !verticalLines[i][j + 1]) { // 가로선을 놓을 수 있는 경우
//System.out.printf("%d단계 (%d, %d) 체크...\n", count, i, j);
verticalLines[i][j] = true; // 가로선 놓기
flag = true; // flag를 true로 초기화
for (int k = 1; k <= N && flag; k++) {
if (!canStraight(k, k, 1)) { // 가리키지 않는 경우
flag = false; // false 설정
break;
}
}
if (flag) { // (1-n) 출발점이 모두 (1-n)번 도착점을 가리킬 경우 (false에 걸리지 않았을 경우)
//System.out.println("성공! ::: " + count);
//return count; // 더 작게 놓을 수 있는 경우가 있을 수 있으므로 바로 반환해선 안됨!
MIN_BRIDGE = Math.min(count, MIN_BRIDGE); // 더 작은 값으로 최소 가로선 설정
} else if (count < Math.min(3, MIN_BRIDGE)) { // 가로선이 3개 미만이거나, 최소 가로선 미만일 경우
selectBridge(count + 1, i); // 가로선 하나 더 놓기 (재귀)
}
verticalLines[i][j] = false; // 볼장 다 보면 방문 해제
}
}
}
}
private static boolean canStraight(int startC, int curC, int curR) { // i번 출발점이 i번 도착점을 가리키는지 검사하는 재귀 함수
if (H < curR) { // 가로선을 다 타고 내려왔을 때
return (startC == curC); // 출발점과 도착점이 같은지에 대한 boolean 반환
}
if (verticalLines[curR][curC]) { // 오른쪽으로 가는 가로선이 존재할 경우
curC++; // 한 칸 오른쪽으로 이동
} else if (verticalLines[curR][curC - 1]) { // 왼쪽으로 가는 가로선이 존재할 경우
curC--; // 한 칸 왼쪽으로 이동
}
return canStraight(startC, curC, curR + 1); // 다음 칸 탐색
}
}
DFS로 하다가 한없이 재귀의 늪으로 들어가버려, 완탐으로 다시 푼 문제.
완탐보다는 부분조합에 더 가까운 것 같다.
DFS로 풀 때는 당연히 1부터 탐색하는 것이 맞지 않나 생각 했다.
그러나 다른 index부터 시작해야 답이 나오는 TC가 있다는 말에... 싹 지우고 다시 고.
괜히 어줍잖게 요령 부리다가 시간이 더 걸린 문제다.
여기서 중요한 건 연속되는 가로선이 없어야 한다는 것이다.
주어진 가로선에 연속되는 가로선을 제하면 생각보다 탐색을 많이 안하게 되는 것이 포인트다.
그리고 또 중요한 것은, 위에서 언급했듯 1번 세로선부터 순차적으로 탐색하며 가로선을 놓게 되면 4%에서 틀렸습니다가 나온다. (저도 알고싶지 않았어요.)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
private static int N, M, H; // 사다리 세로선, 가로선, 가로선 가능 개수
private static boolean[][] verticalLines; // 가로선 존재 여부
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
H = Integer.parseInt(st.nextToken());
if (M == 0) { // 가로선이 없을 경우 체크
System.out.println(0);
return;
}
verticalLines = new boolean[H + 1][N + 1];
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
verticalLines[Integer.parseInt(st.nextToken())][Integer.parseInt(st.nextToken())] = true;
}
int bridge = 0;
for (int i = 1; i <= N; i++) {
bridge += find1Straight(i, i, 1);
if(3 < bridge) {
System.out.println(-1); return;
}
}
System.out.println(bridge);
}
private static int find1Straight(int startC, int curC, int curR) {
if (H < curR) {
return (startC == curC) ? 0 : 4;
}
//System.out.printf("현재 가로선: %d, 현재 세로선: %d, 출발 세로선: %d\n", curR, curC, startC);
int bridge = 4;
if (verticalLines[curR][curC]) curC++; // 오른쪽으로 이동
else if (1 < curC && verticalLines[curR][curC - 1]) curC--;
//System.out.printf("현재 가로선: %d, 현재 세로선: %d, 출발 세로선: %d\n\n", curR, curC, startC);
bridge = Math.min(find1Straight(startC, curC, curR + 1), bridge);
if (bridge < 4) return bridge;
int moveC = curC - 1;
if (0 < moveC && !verticalLines[curR][moveC] && (moveC <= 1 || !verticalLines[curR][moveC - 1]) && (curC == N || !verticalLines[curR][curC])) {
verticalLines[curR][moveC] = true;
bridge = Math.min(1 + find1Straight(startC, moveC, curR + 1), bridge);
if (bridge < 4) return bridge;
verticalLines[curR][moveC] = false;
}
moveC = curC + 1;
if (moveC < N && !verticalLines[curR][curC] && (curC <= 1 || !verticalLines[curR][curC - 1]) && (moveC == N || !verticalLines[curR][moveC])) {
verticalLines[curR][curC] = true;
bridge = Math.min(1 + find1Straight(startC, moveC, curR + 1), bridge);
if (bridge < 4) return bridge;
verticalLines[curR][curC] = false;
}
//System.out.printf("[%d, %d]일 때, 최소 bridge = %d \n", curR, curC, bridge);
return bridge;
}
private static void printVerticalLines() {
int bridge = 0;
for (int i = 1; i <= H; i++) {
for (int j = 1; j <= N; j++) {
System.out.printf("│%1s", (verticalLines[i][j]) ? "─" : " ");
if (verticalLines[i][j]) bridge++;
}
System.out.println();
}
System.out.println();
}
}'알고리즘 및 데이터 구조 > 백준' 카테고리의 다른 글
| [백준] 1600번 : 말이 되고픈 원숭이 (Java) (0) | 2024.03.10 |
|---|---|
| [백준] 15685번 : 드래곤 커브 (Java) (0) | 2024.03.03 |
| [백준] 1937번 : 욕심쟁이 판다 (Java) (4) | 2024.02.28 |
| [백준] 2146번 : 다리 만들기 (Java) (2) | 2024.02.27 |
| [백준] 1068번 : 트리 (Java) (0) | 2024.02.25 |