✅ 문제
14002번: 가장 긴 증가하는 부분 수열 4
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이
www.acmicpc.net
✅ 풀이
import java.io.*;
import java.util.StringTokenizer;
public class Main {
private static int[] nums, count;
private static StringBuilder sb;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
sb = new StringBuilder();
int N = Integer.parseInt(br.readLine());
nums = new int[N + 1];
count = new int[N + 1];
int maxIndex = 0;
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 1; i <= N; i++) {
nums[i] = Integer.parseInt(st.nextToken());
for (int j = i - 1; 0 <= j; j--) { // 현재 숫자 이전의
if (nums[j] < nums[i]) { // 현재 숫자보다 작은
count[i] = Math.max(count[j] + 1, count[i]); // 가장 큰 수열 + 1이 해당 인덱스의 가장 긴 증가하는 수열
if (count[maxIndex] < count[i]) { // 현재까지 가장 긴 수열이라면
maxIndex = i; // 인덱스 저장
}
}
}
}
sb.append(count[maxIndex]).append("\n");
findOrder(maxIndex); // 가장 긴 수열 위치부터 탐색
bw.append(sb.toString());
bw.flush();
bw.close();
br.close();
}
private static void findOrder(int index) {
if (count[index] == 1) { // 수열의 첫 시작에 도착했다면
sb.append(nums[index]).append(" "); // 현재 인덱스의 숫자 출력
return; // 탐색 (완전) 종료
}
for (int i = index - 1; 0 < i; i--) {
if (count[i] == count[index] - 1) { // 직전의 길이 수열이라면
findOrder(i); // 해당 인덱스 방문
sb.append(nums[index]).append(" "); // 현재 인덱스의 숫자 출력
return; // 현재 인덱스 탐색 종료
}
}
}
}
🖨️ 수열의 출력 방법
수열의 길이 체크 자체는 생각보다 어렵지 않다.
(다만, 필자처럼 순환 덜 하겠다고 for문에 아래와 같은 조건문 넣으면 무조건 1%에서부터 틀린다.)
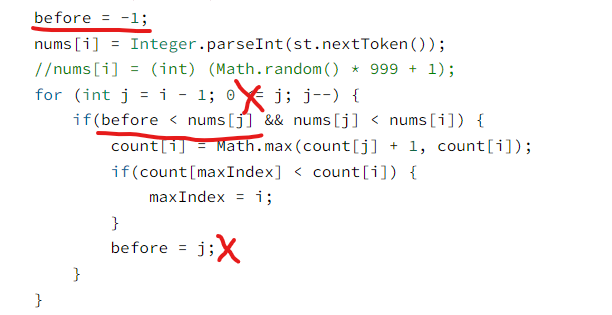
위 코드의 반례 (출처: https://www.acmicpc.net/board/view/130415)
13
3 4 5 6 2 3 1 7 4 3 5 6 7
// answer
6
2 3 4 5 6 7
이 문제에서 조금 생각해봐야 하는 것은 증가하는 수열의 출력이다.
아래와 같은 테스트 케이스를 확인해보자.
6
1 7 3 4 5 6
필자와 같은 방법으로 문제를 풀었다면,
부분 수열의 길이를 저장하는 배열에는 다음과 같이 값이 담겼을 것이다.
| 1 | 2 | 2 | 3 | 4 | 5 |
이 수열을 앞 인덱스부터 시작해 출력하려 한다면,
1 7 4 5 6으로 출력될 수 밖에 없을 것이다.
그렇다면 단순히 증가하는 수열 내 가장 뒤의 숫자부터 판별한다면 부분 수열 길이의 배열을 사용하지 않아도 될까?
아래의 테스트 케이스를 함께 보자
5
2 9 10 4 15
증가하는 부분 수열의 가장 마지막 숫자인 15부터 숫자만으로 판별하게 되면
그 다음 바로 작은 숫자인 4를 지나칠 수 없게 된다.
이를 수열 길이 배열로 확인한다면 다음과 같을 것이다.
| 1 | 2 | 3 | 2 | 4 |
이 배열을 증가하는 부분 수열의 가장 마지막 숫자부터
길이의 수를 감소해나가면서 하나씩 출력한다면 어떻게 될까? (4, 3, 2, 1, ... 이런 식으로)
| 1 | 2 | 3 | 2 | 4 |
증가하는 부분 수열의 길이가 4인 15부터 시작하여
길이가 3인 10, 2인 9, 1인 2까지 하여
이를 나열해보면 결국 정답인 2 9 10 15가 된다.
수열을 찾는 방법과 이를 순서에 맞게 나열하는 법을 알면 어렵지 않은 골드 4의 문제였다.
'알고리즘 및 데이터 구조 > 백준' 카테고리의 다른 글
| [백준] 12110번 2048 (Easy) (Java) (0) | 2024.04.06 |
|---|---|
| [백준] 2011번 : 암호코드 (Java) (0) | 2024.03.26 |
| [백준] 14719번 : 빗물 (Java) (0) | 2024.03.24 |
| [백준] 11000번 : 강의실 배정 (Java) (0) | 2024.03.24 |
| [백준] 4386번 : 별자리 만들기 (Java) (3) | 2024.03.19 |
