🔗 1520번 : 내리막 길
● Java 풀이
● 시간 제한 2초
● 메모리 제한 128 MB
문제
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으며, 각 지점 사이의 이동은 지도에서 상하좌우 이웃한 곳끼리만 가능하다.
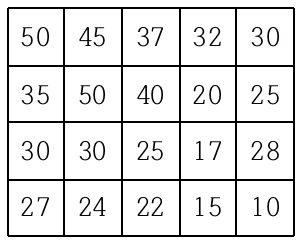
현재 제일 왼쪽 위 칸이 나타내는 지점에 있는 세준이는 제일 오른쪽 아래 칸이 나타내는 지점으로 가려고 한다. 그런데 가능한 힘을 적게 들이고 싶어 항상 높이가 더 낮은 지점으로만 이동하여 목표 지점까지 가고자 한다. 위와 같은 지도에서는 다음과 같은 세 가지 경로가 가능하다.
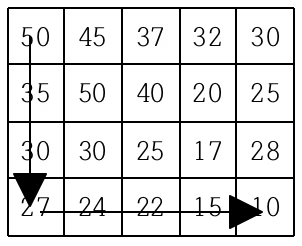
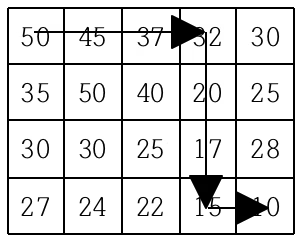
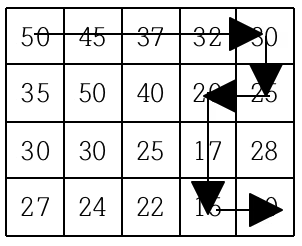
지도가 주어질 때 이와 같이 제일 왼쪽 위 지점에서 출발하여 제일 오른쪽 아래 지점까지 항상 내리막길로만 이동하는 경로의 개수를 구하는 프로그램을 작성하시오.
테스트 케이스
/** 출처 (https://www.acmicpc.net/board/view/120687) **/
// input
4 4
93 72 61 58
90 73 19 49
85 36 75 13
21 41 45 7
// answer
2
// input
7 7
100 33 58 59 61 31 30
74 31 55 62 70 70 29
73 98 49 47 11 10 36
62 59 56 45 44 8 7
59 58 54 53 41 7 3
56 32 29 18 40 4 3
34 31 26 40 39 73 1
// answer
27
/** 출처 (https://www.acmicpc.net/board/view/114555) **/
// input
4 5
10 9 8 5 4
100 100 7 6 3
100 100 100 100 2
100 100 100 100 1
// answer
3
/** 출처 (https://www.acmicpc.net/board/view/108529) **/
// input
5 5
27 26 25 24 23
28 29 30 31 22
17 18 19 20 21
16 32 33 34 35
15 14 13 12 11
// answer
1
/** 출처 (https://www.acmicpc.net/board/view/105277) **/
// input
1 1
1
// answer
1
풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
private static int M, N; // 세로, 가로
private static int[][] map;
private static long[][] canVisit;
private static final int[] dr = {-1, 1, 0, 0}, dc = {0, 0, -1, 1};
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
M = Integer.parseInt(st.nextToken());
N = Integer.parseInt(st.nextToken());
//M = N = 500; // 테스트 케이스
map = new int[M][N];
canVisit = new long[M][N];
for (int i = 0; i < M; i++) {
Arrays.fill(canVisit[i], -1L);
}
canVisit[0][0] = 1;
//int k = 10000;
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < N; j++) {
map[i][j] = Integer.parseInt(st.nextToken());
//map[i][j] = (k--); // 테스트 케이스
}
}
System.out.println(dp(M - 1, N - 1));
}
private static long dp(int r, int c) { // (r, c)까지 도달할 수 있는 경우의 수 구하는 함수
//if(r == 0 && c == 0) return 1;
// 0 이상인 경우로 체크하는 이유는 0이라는 경우의 수도 구할 수 있기 때문
if(0 <= canVisit[r][c]) return canVisit[r][c]; // 해당 위치의 경우의 수를 구했을 경우 그 경우의 수 반환
int mr, mc;
for (int i = 0; i < 4; i++) { // 사방향 탐색
mr = r + dr[i];
mc = c + dc[i];
if (0 <= mr && mr < M && 0 <= mc && mc < N && map[r][c] < map[mr][mc]) { // (mr, mc) 방향에서 (r, c) 방향으로 이동할 수 있을 경우
canVisit[r][c] += dp(mr, mc); // (mr, mc) 방향의 경우의 수 더하기
}
}
return ++canVisit[r][c]; // -1로 초기화 했기 때문에 + 1 해주기
}
private static void print(long[][] arr) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
sb.append(arr[i][j]).append(" ");
}
sb.append("\n");
}
sb.append("\n");
System.out.println(sb);
}
}
풀이 자체는 DP로 어렵지 않았으나, 혹시 DFS로 푼다면 시간 초과가 나니까 조심해야 한다.
시간 초과가 나는지 아닌지 모르겠다면 맥시멈 테스트케이스 값을 하드코딩으로 넣어보자.
테스트 케이스 찾아보다가 DP 배열을 0으로 초기화하면 안되는 이유를 스포 당했다. 하하!
'알고리즘 및 데이터 구조 > 백준' 카테고리의 다른 글
| [백준] 11049번 : 행렬 곱셈 순서 (Java) (0) | 2024.02.23 |
|---|---|
| [백준] 9466번 : 텀 프로젝트 (Java) (0) | 2024.02.22 |
| [백준] 14890번 : 경사로 (Java) (0) | 2024.02.20 |
| [백준] 1005번 : ACM Craft (Java) (0) | 2024.02.19 |
| [백준] 2252번 : 줄 세우기 (Java) (0) | 2024.02.17 |
🔗 1520번 : 내리막 길
● Java 풀이
● 시간 제한 2초
● 메모리 제한 128 MB
문제
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으며, 각 지점 사이의 이동은 지도에서 상하좌우 이웃한 곳끼리만 가능하다.

현재 제일 왼쪽 위 칸이 나타내는 지점에 있는 세준이는 제일 오른쪽 아래 칸이 나타내는 지점으로 가려고 한다. 그런데 가능한 힘을 적게 들이고 싶어 항상 높이가 더 낮은 지점으로만 이동하여 목표 지점까지 가고자 한다. 위와 같은 지도에서는 다음과 같은 세 가지 경로가 가능하다.



지도가 주어질 때 이와 같이 제일 왼쪽 위 지점에서 출발하여 제일 오른쪽 아래 지점까지 항상 내리막길로만 이동하는 경로의 개수를 구하는 프로그램을 작성하시오.
테스트 케이스
/** 출처 (https://www.acmicpc.net/board/view/120687) **/
// input
4 4
93 72 61 58
90 73 19 49
85 36 75 13
21 41 45 7
// answer
2
// input
7 7
100 33 58 59 61 31 30
74 31 55 62 70 70 29
73 98 49 47 11 10 36
62 59 56 45 44 8 7
59 58 54 53 41 7 3
56 32 29 18 40 4 3
34 31 26 40 39 73 1
// answer
27
/** 출처 (https://www.acmicpc.net/board/view/114555) **/
// input
4 5
10 9 8 5 4
100 100 7 6 3
100 100 100 100 2
100 100 100 100 1
// answer
3
/** 출처 (https://www.acmicpc.net/board/view/108529) **/
// input
5 5
27 26 25 24 23
28 29 30 31 22
17 18 19 20 21
16 32 33 34 35
15 14 13 12 11
// answer
1
/** 출처 (https://www.acmicpc.net/board/view/105277) **/
// input
1 1
1
// answer
1
풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
private static int M, N; // 세로, 가로
private static int[][] map;
private static long[][] canVisit;
private static final int[] dr = {-1, 1, 0, 0}, dc = {0, 0, -1, 1};
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
M = Integer.parseInt(st.nextToken());
N = Integer.parseInt(st.nextToken());
//M = N = 500; // 테스트 케이스
map = new int[M][N];
canVisit = new long[M][N];
for (int i = 0; i < M; i++) {
Arrays.fill(canVisit[i], -1L);
}
canVisit[0][0] = 1;
//int k = 10000;
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < N; j++) {
map[i][j] = Integer.parseInt(st.nextToken());
//map[i][j] = (k--); // 테스트 케이스
}
}
System.out.println(dp(M - 1, N - 1));
}
private static long dp(int r, int c) { // (r, c)까지 도달할 수 있는 경우의 수 구하는 함수
//if(r == 0 && c == 0) return 1;
// 0 이상인 경우로 체크하는 이유는 0이라는 경우의 수도 구할 수 있기 때문
if(0 <= canVisit[r][c]) return canVisit[r][c]; // 해당 위치의 경우의 수를 구했을 경우 그 경우의 수 반환
int mr, mc;
for (int i = 0; i < 4; i++) { // 사방향 탐색
mr = r + dr[i];
mc = c + dc[i];
if (0 <= mr && mr < M && 0 <= mc && mc < N && map[r][c] < map[mr][mc]) { // (mr, mc) 방향에서 (r, c) 방향으로 이동할 수 있을 경우
canVisit[r][c] += dp(mr, mc); // (mr, mc) 방향의 경우의 수 더하기
}
}
return ++canVisit[r][c]; // -1로 초기화 했기 때문에 + 1 해주기
}
private static void print(long[][] arr) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
sb.append(arr[i][j]).append(" ");
}
sb.append("\n");
}
sb.append("\n");
System.out.println(sb);
}
}
풀이 자체는 DP로 어렵지 않았으나, 혹시 DFS로 푼다면 시간 초과가 나니까 조심해야 한다.
시간 초과가 나는지 아닌지 모르겠다면 맥시멈 테스트케이스 값을 하드코딩으로 넣어보자.
테스트 케이스 찾아보다가 DP 배열을 0으로 초기화하면 안되는 이유를 스포 당했다. 하하!
'알고리즘 및 데이터 구조 > 백준' 카테고리의 다른 글
| [백준] 11049번 : 행렬 곱셈 순서 (Java) (0) | 2024.02.23 |
|---|---|
| [백준] 9466번 : 텀 프로젝트 (Java) (0) | 2024.02.22 |
| [백준] 14890번 : 경사로 (Java) (0) | 2024.02.20 |
| [백준] 1005번 : ACM Craft (Java) (0) | 2024.02.19 |
| [백준] 2252번 : 줄 세우기 (Java) (0) | 2024.02.17 |