🔗 14890번 : 경사로
● Java 풀이
● 시간 제한 2초
● 메모리 제한 512 MB
문제
크기가 N×N인 지도가 있다. 지도의 각 칸에는 그 곳의 높이가 적혀져 있다.
오늘은 이 지도에서 지나갈 수 있는 길이 몇 개 있는지 알아보려고 한다. 길이란 한 행 또는 한 열 전부를 나타내며, 한쪽 끝에서 다른쪽 끝까지 지나가는 것이다.
다음과 같은 N=6인 경우 지도를 살펴보자.
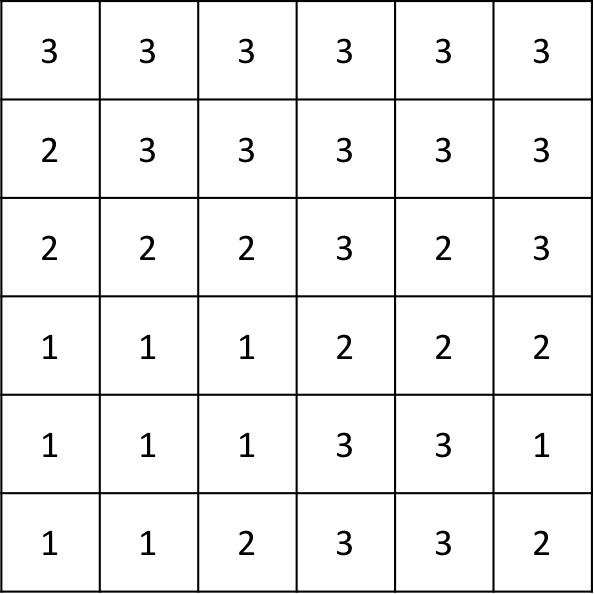
이때, 길은 총 2N개가 있으며, 아래와 같다.

길을 지나갈 수 있으려면 길에 속한 모든 칸의 높이가 모두 같아야 한다. 또는, 경사로를 놓아서 지나갈 수 있는 길을 만들 수 있다. 경사로는 높이가 항상 1이며, 길이는 L이다. 또, 개수는 매우 많아 부족할 일이 없다. 경사로는 낮은 칸과 높은 칸을 연결하며, 아래와 같은 조건을 만족해야한다.
- 경사로는 낮은 칸에 놓으며, L개의 연속된 칸에 경사로의 바닥이 모두 접해야 한다.
- 낮은 칸과 높은 칸의 높이 차이는 1이어야 한다.
- 경사로를 놓을 낮은 칸의 높이는 모두 같아야 하고, L개의 칸이 연속되어 있어야 한다.
아래와 같은 경우에는 경사로를 놓을 수 없다.
- 경사로를 놓은 곳에 또 경사로를 놓는 경우
- 낮은 칸과 높은 칸의 높이 차이가 1이 아닌 경우
- 낮은 지점의 칸의 높이가 모두 같지 않거나, L개가 연속되지 않은 경우
- 경사로를 놓다가 범위를 벗어나는 경우
L = 2인 경우에 경사로를 놓을 수 있는 경우를 그림으로 나타내면 아래와 같다.

경사로를 놓을 수 없는 경우는 아래와 같다.

위의 그림의 가장 왼쪽부터 1번, 2번, 3번, 4번 예제라고 했을 때, 1번은 높이 차이가 1이 아니라서, 2번은 경사로를 바닥과 접하게 놓지 않아서, 3번은 겹쳐서 놓아서, 4번은 기울이게 놓아서 불가능한 경우이다.
가장 위에 주어진 그림 예의 경우에 지나갈 수 있는 길은 파란색으로, 지나갈 수 없는 길은 빨간색으로 표시되어 있으며, 아래와 같다. 경사로의 길이 L = 2이다.
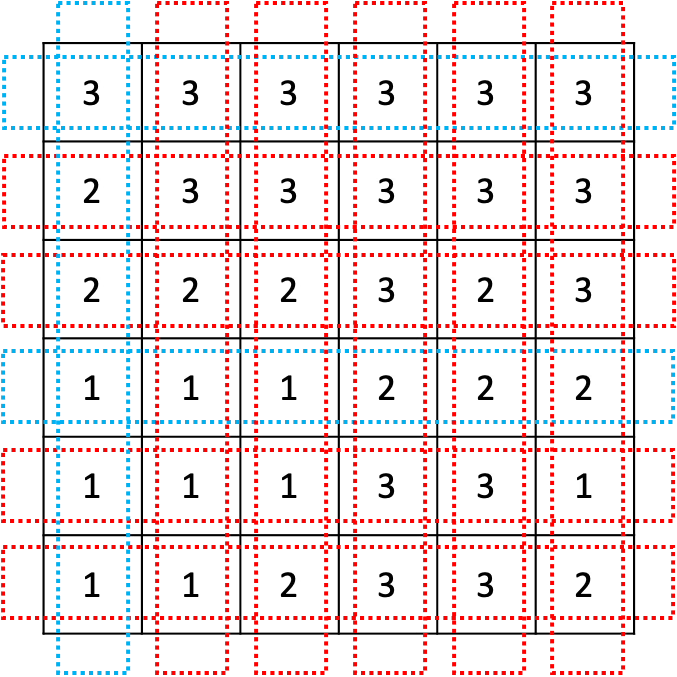
지도가 주어졌을 때, 지나갈 수 있는 길의 개수를 구하는 프로그램을 작성하시오.
풀이
import java.io.*;
import java.util.*;
public class Main {
private static int N, L, LOAD;
private static int[][] map;
private static boolean[][] isStair;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
L = Integer.parseInt(st.nextToken());
map = new int[N][N];
isStair = new boolean[N][N];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < N; j++) {
map[i][j] = Integer.parseInt(st.nextToken());
}
}
horizonCheck();
verticalCheck();
System.out.println(LOAD);
}
private static void horizonCheck() {
isStair = new boolean[N][N];
int canGo;
for (int i = 0; i < N; i++) {
canGo = 1;
for (int j = 1; j < N; j++) {
if(map[i][j] == map[i][j - 1]) continue; // 같은 층일 때
if(1 < Math.abs(map[i][j] - map[i][j - 1])) { // 층 길이가 안 맞을 경우
canGo = 0;
} else if (map[i][j - 1] < map[i][j]) { // 본인이 오르는 층일 때
for (int k = 1; k <= L; k++) { // 계단 세우기
if(j - k < 0 || isStair[i][j - k] || map[i][j - 1] != map[i][j - k]) { // 계단이 벽에 막히거나, 평평하지 않거나, 이미 있을 경우
canGo = 0;
break;
}
isStair[i][j - k] = true;
}
} else { // 내려가는 층일 때
for (int k = 0; k < L; k++) { // 계단 세우기
if(N <= j + k || isStair[i][j + k] || map[i][j] != map[i][j + k]) { // 계단이 벽에 막히거나, 평평하지 않거나, 이미 있을 경우
canGo = 0;
break;
}
isStair[i][j + k] = true;
}
}
if(canGo == 0) break;
}
LOAD += canGo;
}
}
private static void verticalCheck() {
isStair = new boolean[N][N];
int canGo;
for (int i = 0; i < N; i++) {
canGo = 1;
for (int j = 1; j < N; j++) {
if(map[j][i] == map[j - 1][i]) continue; // 같은 층일 때
if(1 < Math.abs(map[j][i] - map[j - 1][i])) { // 층 길이가 안 맞을 경우
canGo = 0;
} else if (map[j - 1][i] < map[j][i]) { // 본인이 오르는 층일 때
for (int k = 1; k <= L; k++) { // 계단 세우기
if(j - k < 0 || isStair[j - k][i] || map[j - 1][i] != map[j - k][i]) { // 계단이 벽에 막히거나, 평평하지 않거나, 이미 있을 경우
canGo = 0;
break;
}
isStair[j - k][i] = true;
}
} else { // 내려가는 층일 때
for (int k = 0; k < L; k++) { // 계단 세우기
if(N <= j + k || isStair[j + k][i] || map[j][i] != map[j + k][i]) { // 계단이 벽에 막히거나, 평평하지 않거나, 이미 있을 경우
canGo = 0;
break;
}
isStair[j + k][i] = true;
}
}
if(canGo == 0) break;
}
LOAD += canGo;
}
}
}
수평 · 수직 확인 로직이 같은데도, 함께 합치는 코드 효율성을 지키지 못한 것 같아 아쉽다.
문제 자체는 매우 쉬웠다. 몇 번의 if문 삽질이 있긴 했지만, 계단이 존재하는지 확인하는 boolean 2차원 배열을 만드니 확실히 쉬웠다. 2차원 배열이 아니더라도, 1차원 배열을 계속 초기화 해서 만들면 더 나으려나 싶다.
'알고리즘 및 데이터 구조 > 백준' 카테고리의 다른 글
| [백준] 11049번 : 행렬 곱셈 순서 (Java) (0) | 2024.02.23 |
|---|---|
| [백준] 9466번 : 텀 프로젝트 (Java) (0) | 2024.02.22 |
| [백준] 1005번 : ACM Craft (Java) (0) | 2024.02.19 |
| [백준] 1520번 : 내리막 길 (Java) (0) | 2024.02.18 |
| [백준] 2252번 : 줄 세우기 (Java) (0) | 2024.02.17 |
🔗 14890번 : 경사로
● Java 풀이
● 시간 제한 2초
● 메모리 제한 512 MB
문제
크기가 N×N인 지도가 있다. 지도의 각 칸에는 그 곳의 높이가 적혀져 있다.
오늘은 이 지도에서 지나갈 수 있는 길이 몇 개 있는지 알아보려고 한다. 길이란 한 행 또는 한 열 전부를 나타내며, 한쪽 끝에서 다른쪽 끝까지 지나가는 것이다.
다음과 같은 N=6인 경우 지도를 살펴보자.

이때, 길은 총 2N개가 있으며, 아래와 같다.

길을 지나갈 수 있으려면 길에 속한 모든 칸의 높이가 모두 같아야 한다. 또는, 경사로를 놓아서 지나갈 수 있는 길을 만들 수 있다. 경사로는 높이가 항상 1이며, 길이는 L이다. 또, 개수는 매우 많아 부족할 일이 없다. 경사로는 낮은 칸과 높은 칸을 연결하며, 아래와 같은 조건을 만족해야한다.
- 경사로는 낮은 칸에 놓으며, L개의 연속된 칸에 경사로의 바닥이 모두 접해야 한다.
- 낮은 칸과 높은 칸의 높이 차이는 1이어야 한다.
- 경사로를 놓을 낮은 칸의 높이는 모두 같아야 하고, L개의 칸이 연속되어 있어야 한다.
아래와 같은 경우에는 경사로를 놓을 수 없다.
- 경사로를 놓은 곳에 또 경사로를 놓는 경우
- 낮은 칸과 높은 칸의 높이 차이가 1이 아닌 경우
- 낮은 지점의 칸의 높이가 모두 같지 않거나, L개가 연속되지 않은 경우
- 경사로를 놓다가 범위를 벗어나는 경우
L = 2인 경우에 경사로를 놓을 수 있는 경우를 그림으로 나타내면 아래와 같다.

경사로를 놓을 수 없는 경우는 아래와 같다.

위의 그림의 가장 왼쪽부터 1번, 2번, 3번, 4번 예제라고 했을 때, 1번은 높이 차이가 1이 아니라서, 2번은 경사로를 바닥과 접하게 놓지 않아서, 3번은 겹쳐서 놓아서, 4번은 기울이게 놓아서 불가능한 경우이다.
가장 위에 주어진 그림 예의 경우에 지나갈 수 있는 길은 파란색으로, 지나갈 수 없는 길은 빨간색으로 표시되어 있으며, 아래와 같다. 경사로의 길이 L = 2이다.

지도가 주어졌을 때, 지나갈 수 있는 길의 개수를 구하는 프로그램을 작성하시오.
풀이
import java.io.*;
import java.util.*;
public class Main {
private static int N, L, LOAD;
private static int[][] map;
private static boolean[][] isStair;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
L = Integer.parseInt(st.nextToken());
map = new int[N][N];
isStair = new boolean[N][N];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < N; j++) {
map[i][j] = Integer.parseInt(st.nextToken());
}
}
horizonCheck();
verticalCheck();
System.out.println(LOAD);
}
private static void horizonCheck() {
isStair = new boolean[N][N];
int canGo;
for (int i = 0; i < N; i++) {
canGo = 1;
for (int j = 1; j < N; j++) {
if(map[i][j] == map[i][j - 1]) continue; // 같은 층일 때
if(1 < Math.abs(map[i][j] - map[i][j - 1])) { // 층 길이가 안 맞을 경우
canGo = 0;
} else if (map[i][j - 1] < map[i][j]) { // 본인이 오르는 층일 때
for (int k = 1; k <= L; k++) { // 계단 세우기
if(j - k < 0 || isStair[i][j - k] || map[i][j - 1] != map[i][j - k]) { // 계단이 벽에 막히거나, 평평하지 않거나, 이미 있을 경우
canGo = 0;
break;
}
isStair[i][j - k] = true;
}
} else { // 내려가는 층일 때
for (int k = 0; k < L; k++) { // 계단 세우기
if(N <= j + k || isStair[i][j + k] || map[i][j] != map[i][j + k]) { // 계단이 벽에 막히거나, 평평하지 않거나, 이미 있을 경우
canGo = 0;
break;
}
isStair[i][j + k] = true;
}
}
if(canGo == 0) break;
}
LOAD += canGo;
}
}
private static void verticalCheck() {
isStair = new boolean[N][N];
int canGo;
for (int i = 0; i < N; i++) {
canGo = 1;
for (int j = 1; j < N; j++) {
if(map[j][i] == map[j - 1][i]) continue; // 같은 층일 때
if(1 < Math.abs(map[j][i] - map[j - 1][i])) { // 층 길이가 안 맞을 경우
canGo = 0;
} else if (map[j - 1][i] < map[j][i]) { // 본인이 오르는 층일 때
for (int k = 1; k <= L; k++) { // 계단 세우기
if(j - k < 0 || isStair[j - k][i] || map[j - 1][i] != map[j - k][i]) { // 계단이 벽에 막히거나, 평평하지 않거나, 이미 있을 경우
canGo = 0;
break;
}
isStair[j - k][i] = true;
}
} else { // 내려가는 층일 때
for (int k = 0; k < L; k++) { // 계단 세우기
if(N <= j + k || isStair[j + k][i] || map[j][i] != map[j + k][i]) { // 계단이 벽에 막히거나, 평평하지 않거나, 이미 있을 경우
canGo = 0;
break;
}
isStair[j + k][i] = true;
}
}
if(canGo == 0) break;
}
LOAD += canGo;
}
}
}
수평 · 수직 확인 로직이 같은데도, 함께 합치는 코드 효율성을 지키지 못한 것 같아 아쉽다.
문제 자체는 매우 쉬웠다. 몇 번의 if문 삽질이 있긴 했지만, 계단이 존재하는지 확인하는 boolean 2차원 배열을 만드니 확실히 쉬웠다. 2차원 배열이 아니더라도, 1차원 배열을 계속 초기화 해서 만들면 더 나으려나 싶다.
'알고리즘 및 데이터 구조 > 백준' 카테고리의 다른 글
| [백준] 11049번 : 행렬 곱셈 순서 (Java) (0) | 2024.02.23 |
|---|---|
| [백준] 9466번 : 텀 프로젝트 (Java) (0) | 2024.02.22 |
| [백준] 1005번 : ACM Craft (Java) (0) | 2024.02.19 |
| [백준] 1520번 : 내리막 길 (Java) (0) | 2024.02.18 |
| [백준] 2252번 : 줄 세우기 (Java) (0) | 2024.02.17 |